Úvod do teorie kombinatorických her

Einige Methoden des Schaffens der ästhetisch wirken den Computerbilder.

Wenn auch der Computer die heutige Gesellschaft revolutionär beeinflußt, so läßt sich dies in Hinblick auf die Kunst zunächst nicht sagen. In das Gebiet der Kunst drang der Computer trotz -- oder wegen -- seines hohen technischen Standards nur behutsam ein. Doch in den letzten dreißig Jahrenentstand ein ganzes Gebiet der Kunst, das man Computerkunst nennt. Unter Computerkunst versteht man die Kunst, die auf irgendeine Weise mit Hilfe eines Computers generiert wird, sei es mittels Software in Form von Programmen oder mittels Hardwarein Form des Bildschirms oder anderer Peripheriegeräte. Es gibt zahlreiche Möglichkeiten, den Computer in diesem Gebiet einzusetzen. Stets aber ist es der Künstler, der Initiator einer Bildidee ist, so daß  Computerkunst streng genommen computerunterstützte Kunst ist (von da auch CAA = Computer Aided Art stammt).

       
         
           

Wie gewisse Naturobjekte unsere Fantasie besoders anregen (in der Kunstterminologie nennt man sie "objects trouvés" = "gefundene" Objekte), so können es ebenso einige mathematische Objekte oder Prozesse machen. Aber diese mathematische Objekte und Prozesse im Unterschied von Natur objekten sind immateriell und also unsichtbar, so daß  mansie zuerst visualisieren muß. Diese Visualisation kann man auf viel, viel verschiedene Weise realisieren. Dabei interessieren wir uns aber nicht für alle, sondern nur für möglichst ästhetische Realisationen dieser immateriellen Objekte.

Bemerken wir noch, daß  Mathematik als ein abstraktes Wissenschaftsgebiet mit ästhetik nichts gemein hat, erst die Konkretisierung ihrer immateriellen Objekte erlaubt zu behaupten, daß   ästhetik in der Mathematik latent angelegt ist.

Das Ziel unseres Artikels ist einige von vielen Verfahren der Visualisationen der mathematischen Objekte und Methoden ausführlicher zu zeigen und zu diskutieren. In diesem Sinn ist diese Arbeit eine freie Fortsetzung von der Arbeit [1].

Wir machen noch eine Bemerkung zu dieser zitierten Arbeit. Die erste Methode des Schaffens der Computerbilder, die in [1] beschrieben ist (I gruppo, esempio 1 -- 4), derenInhalt --- kurz gesagt --- eine zufällige Füllung des Qadratnetzses mit vorgewählten graphischen Elementen enthält, ist eine Vereinfachung der Methode, die tschechischer Künstler Z. Sýkora benutzte. Seine Methode ist beschrieben zum Bespiel in [2]. Fig. 1 zeigtein Sýkoras Bild aus der Epoche der 60. Jahren seines Schaffens. Es handelt sich um "Schwarz-weiß Strukture", 1965, 220 × 160 cm, die jetztin Eigentum der Nationalgalerie Berlin ist. Sýkora blieb auch in weiteren Jahren der eng mit Computer verbundenen Kunst treu. über sein weiteres Shaffen kann man zum Beispiel im Buch [3] (Seiten 189 -- 195 und andere) die Informationen finden.

Das Problem besteht also darin, jedem Punkt  (c, r),  (0 L c < 640,  0 L r < 480 )  eine ganze Zahl  p(c,r),  (0 L p(c,r) < 16 ) zuordnen,so daß  man den sogenanntenPixel  (c, r, p(c,r) )  bekommt, der den Attribut und also auch die Farbe des Punktes  (c, r)  des Bildschirms beeinflußt.

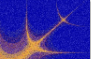
Bei der ersten Methode, die wir zeigen wollen, handelt es sich um eine passende Visualisation der Objekte, die Funktionen f(x,y) von zwei reellen Veränderlichen x, y oder Funktionen j (z) = j (x + iy) einer komplexen Veränderliche z = x + iy sind.

Der Benützer des Programms wählt zuerst den Punkt (x0, y0) dem die linke untere Ecke des Bildschirms (die wir mit (0, 0) bezeichnen, also für  c = r = 0) entspricht und weiter wählt er noch die Differenz d . Jedem Punkt

(x0 + cd,y0 + rd),    0 L c <640,   0 L r < 480
wird dann der Punkt  (c, r)  des Bildschirms zugeordnet. Man mu\ss  natürlich darauf achtgeben, daß  alle benützte Punkte im Definitionsbereich der Funktion f(x, y) liegen. Der Benützer wählt noch eine für das ganze Programm feste Zahl m und  p(c, r)  wird dann nach der folgenden Formel gerechnet
p(c, r) o [f(x0 + cd, y0 + rd)]    ( mod   m),
wo die eckige Klammern [a] sogenannten ganzen Teil der Zahl a bezeichnen. Also  p(c,r)  ist der kleinste nicht negative Rest nach der Division von der ganzen Zahl  [f(x0+cd,y0+rd)]  durch m , so da\ss
p(c,r) = 0, 1, 1 , m-1.
Im Falle der komplexen Funktion j (z) kann man folgende Formelbenützen: für jede 0 L c < 640 und jede 0 L r < 480 ist
p(c,r) o [|j (x0+cd + (y0+rd)i)|]    ( mod   m),
eventuell
p(c,r) o [|j (x0+cd + (y0+rd)i)|2 ]    ( mod   m),
wenn man den n Wurzel beim Rechnen den absoluten Betrag der komplexenZahl meiden will (diesen n Fall der komplexen Funktion j (z) kann man natürlich immer auf den ersten Fall der Funktion f(x,y) überführen).

Eben beschriebene Methode erlaubt breite Anwendungen durch zahlreiche Möglichkeiten der Wahl der Funktion f(x,y) oder j (z), sowie auch die Möglichkeiten der Wahl des "Ausschnittes"des Definitionbereiches der Funktion (die Wahl des "Anfangspunktes" (x0,y0) )  und der"Vergröß erung" d . Wichtige Rolle spielt ebenso die Wahl des Moduls m .

Noch eine weitere Grupe von Tatsachen beeinflußt das endliche Ergebnis: die Wirkungen, die mit Hardware des gebrauchten Computers verbunden sind. Konkret sind das hauptsächlich die Einflüsse auf Bildergebnis, die entweder durch die Form der Aufzeichnung der Zahlen in Computerspeicheroder durch die Form der Ausrechnung der gebrauchten Standardfunktionen verursacht werden. Man kann natürlich diese Tatsachen auch zielstrebig zur Beeinflußung des Ergebnisses ausnutzen.

Als Beispiel des "Versagens" der Standardfunktion nehmen wir die Funktion j (z) = z3 . Bei Rechnung der Zahl p(c,r) in der Form

p = p(c,r) o [|j (x0 + cd + (y0 + rd)i)|2 ]    (mod   16),
arbeitet die Funktion "ganzer Teil" bei wachsendem |z| = |x0 + cd + (y0 + rd)i| immer"schlechter". Für kleine Wertevon |z| kann p alle Werte aus der ganzen Menge { 0, 1, 1 , 15 } der Reste annehmen (also für solche z bekommtman alle 16 mögliche Attribute -- Farben), für größere |z| gibt in einigen Fällen unsere Funktion falsche Ergebnisse, sodaß   p = 1, 2, 4, 6, 8, 10, 12 oder 14  (man bekommt nur 8 möglicheFarben), weiter nur 4, dann 2 und endlich (für |z| > 22.627 1 ) istimmer p = 0. Das kann man auf Fig. 2 sehen (vielleicht auch einzige Zwischenringe mit verschiedener Anzahl von Farben). Also wenn wir die Funktion j (z) = z3 durch beschriebene Weise visualisierenwollen, müssen wir solchen Abschitt der komplexen Ebene wählen, der innerhalb des Kreises |z| < 22.627 1 liegt, wenn auch Definitionsbereich unser Funktion die ganze komplexe Ebene ist. Wir können kurz sagen,daß  der "Visualisationsbereich" der betrachteten Funktiondieser Kreis ist.

Man kann natürlich diese Situation zur Realisation der Bildideeausnutzen: man kann entweder im Bereich mit vielen Farben arbeiten, oder im Gegenteil ein "ruhiges" Bild mit wenig Farben aussuchen. Einige Bespiele kann man in folgenden Figuren 3 -- 5 sehen, in denen gleichzeitig die Rolle der "Vergröß erung" d gezeigt wird (es handelt sich in allen Figuren umdieselbe Funkton j (z) = z3 ). Zur jeder Figur sinddie Koordinatendes "Anfangspunktes" (x0, y0) und die "Vergrö\sserung" d gegeben: für Fig. 3 ist z0 = 3 + 3i und d = 0.001, fürFig. 4 ist z0 = -3 - 17i und d = 5.10-8 und für Fig. 5, dieden übergang zwischen vier-- und zweifarbigem Gebiet zeigt, ist z0 = -11.9998 - 16.1984i und d = 10-7 .

Verschiedene Funktionen haben natürlich auch seine Visualisationsbereiche oft ganz verschieden. Zum Beispiel Fig. 6 zeigt Visualisationsbereich für die Funktion j (z) = z5 , Fig. 7für j (z) = sin z und Fig. 8 für eine Funktion f(x,y), die in Polynom von 8. Grad ist.

* * *

Zweite Methode, die wir jetzt zeigen wollen, ist eigentlich nur eine gewisse Modifkation der ersten Methode, doch aber bedeutet eine wesentliche Bereicherung unserer Möglichkeiten beim Schaffen der Computerbilder. Eshandelt sich wieder um die Visualisation der mathematischen Funktionen der Form f(x,y) oder j (z). Man wählt wie bei derersten Methode den "Anfangspunkt" (x0, y0) und den Schritt d, aberanstatt Modul m, wählt man eine Menge {m1, m2, 1 , mk } von der ganzen positiven Zahlen, wo 1 < k < 16. Wir bezeichnen mit A(c, r) die passende aus der Zahlen

[f(x0+cd,y0+rd)],  [|j (x0+cd+(y0+rd)i)|],  [| j(x0+cd+(y0+rd)i)|2 ]
und den Wert p(c, r) rechnen wir auf folgende Weise aus: p(c, r) = i,  wenn der Index  i Î { 1, 2, 1 , k },  die kleinste Zahl ist, für welche A(c, r) o 0  ( mod  mi) gilt, das heißt, ertfür alle  j,  1 L j < i  immer  A(c, r)¬ o 0  ( mod  mj)   gilt. Wenn ein solcher Index  i   nicht existiert, wir legen   p(c, r) = 0.

Interssante Ergebnisse bekommt man, wenn für die Zahlen m1, m2, 1 verschiedene Primzahlen gewählt werden. Natürlich auch die Reihenfolge der Zahlen m1, m2, 1 kann den Bild beeinflussen.

* * *

Dritte Methode besteht in Folgendem: Man wählt zuerst einige Gebiete G1, G2, 1 Gk von den Punkten (x, y) (so da\ss  0 L x < 640,  0 L y < 480 ) und zu jedem Gebiet Gi ordnetman eine Farbe coli zu. Weiter wählt man eine Differenz d und Anzahl der Iterationen n . Man konstruiert jetzt eine Folge

(x0,y0,col0), (x1,y1,col1), 1, (xn,yn,coln)
von Pixeln, so daß  (x0,y0) ein beliebiger Punkt ist (z.B. x0 = 320,  y0 = 240 ) und col0 = 0 (schwarz). Sei jetzt (xi,yi,coli) bekannt. Man wählt zufällig ein Gebiet Gj und (wenn Gj mehrere Punkte enthält), wählt man noch zufällig einen Punkt (u,v) Î Gj.  Dann legt man
coli+1 = colj,  xi+1 =
xi + u
d
,  yi+1 =
yi +v
d
,
und zeichnet auf dem Bilschirm den Punkt (xi+1,yi+1) mit der Farbe coli+1. Der Process  endet mit i = n . Die Zahl d beeinflußt die Schärfe des Bildes (s. die Fig. 9, wo d = nn und Fig. 10, wo d = 10 ). Die Zahl m beeinflußt  dieGröße des Bildes auf dem Bildschirm.

Auch diese Methode begleiten wir mit einem Programm, in dem die gegebene Gebiete Gi einpunktige Mengen sind (und zwar die Gipfel drei konzentrischen regelmässigen n -ecken). Die Farben, welche einigen Gebieten zugeordnet werden, sind mit Hilfe des Fieldes s(n) gegeben.

* * *

Als vierte Methode kann man eine gewisse Zusammenfassung vonder ersten, eventuell zweiten Methode mit der letzten bezeichnen. Beidieser Methode wählt man in jedem Schritt zufällig die Koordinaten u, v   (0 L u < 640,   0 L v < 480 ) und berechnet nach derMethode 1 oder 2 (bei gegebener Funktion f(x,y), Anfangspunkt (x0,y0) und Schritt passo ) die Farbe col, die dem Punkt (u,v) gehört. Man zeichnet aber nicht den Pixel (u,v,col), sondern den Pixel (xi,yi,col), wo die Koordinaten xi, yi nachder dritten Methode aus der Zahlen u, v gerechnet werden.

* * *
  1. J. Blažek, C. Sitia: Un contributo all'educazione esteticamediante l'elaboratore, L'insegnamento della matematicae delle scienzeintegrate, Vol. 3, No. 8, 1990, S. 756 -- 782. -- überdruck in Quaderno di aggiornamentoper operatori della formazione professionale, N. 10, 1991,. S. 39 -- 79.
  2.  Z. Sýkora, J. Blažek: Computer - aided multielement geometrical abstract paintings, Leonardo, Vol. 3, No. 4, S. 409 -- 413. -- überdruckin Visual Art, Matematics and Computers: Selections from the Journal Leonardo, Pergamon Press, 1977, pp.261 -- 265.
  3.  E. Steller: Computer und Kunst, BI Wissenschaftsverlag, 1992.